Can you Deep Learn the Stock Market?

You can read the complete study at the following links:  

 

DNN Stock Market Study at SlidesFinder 

DNN Stock Market Study at Slideshare 

 

 

Objectives:

We will test whether: 

 

a) Sequential Deep Neural Networks (DNNs) can predict the stock market better than OLS regression;

b) DNNs using smooth Rectified Linear Unit activation functions perform better than the ones using Sigmoid (Logit) activation functions. 

 

Data:

Quarterly data from 1959 Q2 to 2021 Q3.  All variables are fully detrended as quarterly % change or first differenced in % (for interest rate variables).  Models are using standardized variables.  Predictions are converted back into quarterly % change.  

 

Data sources are from FREDS for the economic variables, and the Federal Reserve H.15 for interest rates.

 

Software used for DNNs.

R neuralnet package.  Inserted a customized function to use a smooth ReLu (SoftPlus) activation function.   

 

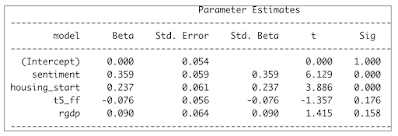
The variables within the underlying OLS Regression models are shown within the table below: 

 

Consumer Sentiment is by far the most predominant variable.  This is supported by the behavioral finance (Richard Thaler) literature.  

 

Housing Start is supported by the research of Edward E. Leamer advancing that the housing sector is a leading indicator of overall economic activity, which in turn impacts the stock market. 

 

Next, the Yield Curve (5 Year Treasury minus FF), and economic activity (RGDP growth) are well established exogenous variables that influence the stock market.  Both are not quite statistically significant.  And, their influence is much smaller than for the first two variables.  Nevertheless, they add explanatory logic to our OLS regression fitting the S&P 500. 

 

The above were the best variables we could select out of a wide pool of variables including numerous other macroeconomic variables (CPI, PPI, Unemployment rate, etc.) interest rates, interest rate spreads, fiscal policy, and monetary policy (including QE) variables. 

 

Next, let's quickly discuss activation functions of hidden layers within sequential Deep Neural Networks (DNN) model.  Until 2017 or so, the preferred activation function was essentially a Logit regression called Sigmoid function.

 

There is nothing wrong with the Sigmoid function per se.  The problem occurs when you take the first derivative of this function.  And, it compresses the range of values by 50% (from 0 to 1, to 0 to 0.5 for the first iteration).  In iterative DNN models, the output of one hidden layer becomes the input for the sequential layer.  And, this 50% compression from one layer to the next can generate values that converge close to zero.  This problem is called the “vanishing gradient descent.”  

 

Over the past few years, the Rectified Linear function, called ReLu, has become the most prevalent activation function for hidden layers.  We will advance that the smooth ReLu, also called SoftPlus is actually much superior to ReLu. 

 

 

SoftPlus appears superior to ReLu because it captures the weights of many more neurons’ features, as it does not zero out any such features with input values < 0.  Also, it generates a continuous set of derivatives values ranging from 0 to 1.  Instead, ReLu derivatives values are limited to a binomial outcome (0, 1). 

 

Here is a picture of our DNN structure. 

 

• One input layer with 4 independent variables: Consumer Sentiment, Housing Start, Yield Curve, and RGDP. 

 

• Two hidden layers.  The first one with 3 nodes, and the second one with 2 nodes.  Activation function for the two hidden layers are SoftPlus for the 1st DNN model, and Sigmoid for the second one.

 

• One output variable, with one node, the dependent variable, the S&P 500 quarterly % change.  The output layer has a linear activation function. 

 

• The DNN loss function is minimizing the sum of the square errors (SSE).  Same as for OLS.  

 

The balance of the DNN structure is appropriate.  It is recommended that the hidden layers have fewer 

nodes than the input one; and, that they have more nodes than the output layer.  Given that, the choice of 

nodes at each layer is just about predetermined.  More extensive DNNs would not have worked anyway.   

This is because the DNNs, as structured, already had trouble converging towards a solution given an 

acceptable error threshold. 

 

As expected the DNN models have much better fit with the complete historical data than the OLS 

Regression. 

 

 

As seen above, despite the mentioned limitation of the Sigmoid function, the two DNN models (SoftPlus 

vs. Sigmoid) relative performances are indistinguishable.  And, they are both better than OLS Regression.

 

But, fitting historical data and predicting or forecasting on an out-of-sample or Hold Out test basis are two 

completely different hurdles.  Fitting historical data is a lot easier than forecasting.

 

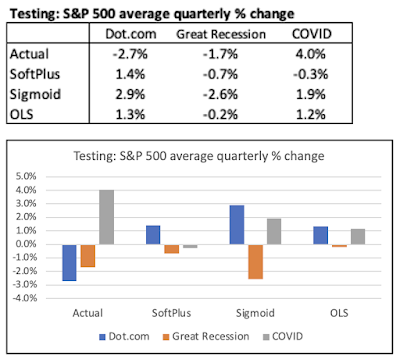
We will use three different Test periods as shown in the table below:

 

 

Each testing period is 12 quarters long.  And, it is a true Hold Out or out-of-sample test.  The training data 

consists of all the earlier data from 1959 Q2 up to the onset of the Hold Out period.  Thus, for the 

Dot.com period, the training data runs from 1959 Q2 to 2000 Q1.

 

The quarters highlighted in orange denote recessions.  We call the three periods, Dot.com, Great 

Recession, and COVID periods as each respective period covers the mentioned events.

 

To visualize the models' respective prediction performance, we will use "skylines."  The column graph 

below looks like a set of skylines with vertical buildings for positive values and reflection in water for 

negative values.  Within the complete linked study, we show several other ways to convey the forecasting 

performance that you may prefer.  

 

 

As shown above, all the models predictions are really pretty dismal.  None of the models predicted the 

protracted 3-year Bear market associated with the Dot.com bubble.  At the margin, the OLS model

actually performed a bit better than the DNN models.  

Now, let's look at the Great Recession period.  In this situation, the models did better.  However, their 

overall predicting performance was nothing to write home about.  All models completely missed the 

severe market correction in the third year of the Great Recession period.  And, again the DNN models did 

not perform any better than the OLS Regression.

 

When focusing on the COVID period, the ongoing mediocrity (at best) of the models' prediction 

performance is readily apparent.  All models completely missed the robust Bull market in the third year of 

the COVID period (as defined).  Again, the DNN models did not fare any better than the simpler OLS 

Regression.  

 

If we look at average predictions for all three models for all three testing periods, we can get a quick 

snapshot of the competitiveness of the models. 

 

Without getting bogged down into attempting to fine tune model rankings between these three models, we can still derive two takeaways.  

The first one is that the Sigmoid issue with the "vanishing gradient descent" did not materialize.  As shown, the Sigmoid DNN model actually was associated with greater volatility in average S&P 500 quarterly % change than for the SoftPlus DNN model.   

The second one is that the DNN models did not provide any prediction incremental benefits over the simpler OLS Regression.  

So, why did all the models, regardless of their sophistication, pretty much fail in their respective predictions? 

It is for a very simple reason.  All the relationships between the Xs and Y variables are very unstable.  The table below shows the correlations between such variables during the Training and Testing periods.  As shown, many of the correlations are very different between the two (Training and Testing).  At times, those correlations even flip signs (check out the correlations with the Yield Curve (t5_ff)).  

The models' predictions failing is especially humbling when you consider that the mentioned 3-year Hold Out tests still presumed you had perfect information over the next 3 years regarding the four X variables.  As we know, this is not a realistic assumption.  

 

 

 

 

 

Can Treasury Inflation Protected Securities (TIPS) predict Inflation?

 Treasury Yield - TIPS Yield = Inflation Expectation

The above basic equation allows to derive long term Inflation Expectation from the bond market.  By looking at the spread between Treasuries and TIPS of identical maturities, we can derive inflation expectation over a 5 year, 7 year, and 10 year horizon. 

The TIPS data is unfortunately very limited and starts only in 2003.  However, given that we deal with monthly observations the data is still associated with numerous data points. 

So back in 2003, we could derive annualized 5 year, 7 year, and 10 year inflation expectations by looking at the spread between the matching Treasuries and TIPS. 

In 2003, we derived annualized 5 year expectation over the 2003- 2008 period.  And, we compare this inflation expectation with the actual annualized 5 year inflation rate over this same 2003 - 2008 period observed in 2008.  So, when we graph this data, the first observation will start in 2008.  

When looking at the 7 year expectation, the framework is the same as the above.  And, when we graph this data, the first observation will start in 2010.  For 10 year inflation expectation, the first observation will be in 2013.

The complete study can be found at the following link: 

TIPS study at Slideshare  

TIPS study at SlidesFinder 

None of the TIPS derived inflation expectations turned out into effective predictions as shown on the scatter plots below. 

The scatter plots are more readily visible within the complete study.  Nevertheless, at a high level these three scatter plots disclose images of near randomness.  This is true whether you look at 5 year, 7 year, or 10 year horizons.  In all three cases, the underlying linear regressions have a slope and an R Square close to Zero denoting near randomness and absence of any material relationship between inflation expectation and actual inflation years later.

Here is looking at the 5 year horizon.

 

Here is looking at the 7 year horizon.

Here is looking at the 10 year horizon. 

All three graphs have a similar pattern with little relationship between inflation expectation and actual inflation.  This absence of relationship was precisely diagnosed using the scatter plots and underlying linear regressions above.  

When we combine the 3 sets of inflation predictions on the same graph, we can observe how bond investors reacted to the onset of the Great Recession back in 2008. 

 

The graph above discloses that back in 2008, the spread between Treasuries and TIPS over the 5 year, 7 year, and 10 year maturities resulted in inflation prediction associated with a deep deflationary environment.  We can observe that with the 3 deep negative spikes denoting negative inflation expectation over long periods of time starting back in 2008.  

Back in 2008, the negative inflation expectation over the 5 year horizon kicked in 2013 (blue line); 

Over the 7 year horizon it kicked in 2015 (red line); and 

Over the 10 year horizon it kicked in 2018 (gray line).  

Next, let's compare the combined inflation expectations as presented above vs. what happened: the actual inflation over those respective periods. 

As shown above, the actual annualized inflation rates look completely different from the matching annualized inflation expectations.  Within the actual data, there are no downward spike associated with a deflationary environment over several years (each monthly data point covers several years of data associated with the various maturities of the bonds: 5 year, 7 year, and 10 year).

There are considerations that the Federal Reserve (Fed) is a dominant investor in TIPS.  And, therefore the Fed may have distorted the resulting inflation expectation measure.  If that is the case, TIPS yields would be lower than otherwise.  And, the resulting inflation expectations would be higher than otherwise.  This is counter to the objective of the Fed.  But, this may be an unintended consequence that the Fed has not resolved.  

Looking at the data is rather ambivalent. 

The 7 year and 10 year maturities are supportive of the hypothesis that the Fed may have influenced the TIPS yields downward and indirectly the inflation expectations upward.  For both maturities, the inflation expectations are in average statistically significantly higher than actual inflation.  However, when looking the 5 year maturity, this is not the case; as actual inflation in average has been a bit higher than inflation expectation.