You can read the complete study at the following links:
DNN Stock Market Study at SlidesFinder
DNN Stock Market Study at Slideshare
Objectives:
We will test whether:
a) Sequential
Deep Neural Networks (DNNs) can predict the stock market better than OLS
regression;
b) DNNs
using smooth Rectified Linear Unit activation functions perform better than the ones
using Sigmoid (Logit) activation functions.
Data:
Quarterly data from 1959 Q2 to 2021
Q3. All variables are fully detrended as
quarterly % change or first differenced in % (for interest rate
variables). Models are using standardized
variables. Predictions are converted
back into quarterly % change.
Data sources are from FREDS for the
economic variables, and the Federal Reserve H.15 for interest rates.
Software
used for DNNs.
R neuralnet package. Inserted a customized function to use a
smooth ReLu (SoftPlus) activation function.
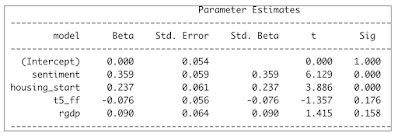
The variables within the underlying OLS Regression models are shown within the table below:
Consumer Sentiment is by far the most
predominant variable. This is supported
by the behavioral finance (Richard Thaler) literature.
Housing Start is supported by the research
of Edward E. Leamer advancing that the housing sector is a leading indicator of
overall economic activity, which in turn impacts the stock market.
Next, the Yield Curve (5 Year Treasury
minus FF), and economic activity (RGDP growth) are well established exogenous
variables that influence the stock market.
Both are not quite statistically significant. And, their influence is much smaller than for
the first two variables. Nevertheless,
they add explanatory logic to our OLS regression fitting the S&P 500.
The above were the best variables we could select out of a wide pool of variables including numerous other macroeconomic variables (CPI, PPI, Unemployment rate, etc.) interest rates, interest rate spreads, fiscal policy, and monetary policy (including QE) variables.
Next, let's quickly discuss activation functions of hidden layers within sequential Deep Neural Networks (DNN) model. Until 2017 or so, the preferred activation function was essentially a Logit regression called Sigmoid function.
There is nothing wrong with the Sigmoid
function per se. The problem occurs when
you take the first derivative of this function.
And, it compresses the range of values by 50% (from 0 to 1, to 0 to
0.5 for the first iteration). In
iterative DNN models, the output of one hidden layer becomes the input for the
sequential layer. And, this 50%
compression from one layer to the next can generate values that converge close
to zero. This problem is called the
“vanishing gradient descent.”
Over the past few years, the Rectified Linear function, called ReLu, has become the most prevalent activation function for hidden layers. We will advance that the smooth ReLu, also called SoftPlus is actually much superior to ReLu.
SoftPlus appears superior to ReLu because
it captures the weights of many more neurons’ features, as it does not zero out
any such features with input values < 0.
Also, it generates a continuous set of derivatives values ranging from 0
to 1. Instead, ReLu derivatives values
are limited to a binomial outcome (0, 1).
Here is a picture of our DNN structure.
• One
input layer with 4 independent variables: Consumer Sentiment, Housing Start,
Yield Curve, and RGDP.
• Two
hidden layers. The first one with 3
nodes, and the second one with 2 nodes.
Activation function for the two hidden layers are SoftPlus for the 1st DNN model, and Sigmoid for the second
one.
• One
output variable, with one node, the dependent variable, the S&P 500
quarterly % change. The output layer has
a linear activation function.
• The
DNN loss function is minimizing the sum of the square errors (SSE). Same as for OLS.
The balance of the DNN structure is
appropriate. It is recommended that the
hidden layers have fewer
nodes than the input one; and, that they have more
nodes than the output layer. Given that,
the choice of
nodes at each layer is just about predetermined. More extensive DNNs would not have worked
anyway.
This is because the DNNs, as
structured, already had trouble converging towards a solution given an
acceptable error threshold.
As expected the DNN models have much better fit with the complete historical data than the OLS
Regression.
As seen above, despite the mentioned limitation of the Sigmoid function, the two DNN models (SoftPlus
vs. Sigmoid) relative performances are indistinguishable. And, they are both better than OLS Regression.
But, fitting historical data and predicting or forecasting on an out-of-sample or Hold Out test basis are two
completely different hurdles. Fitting historical data is a lot easier than forecasting.
We will use three different Test periods as shown in the table below:
Each testing period is 12 quarters
long. And, it is a true Hold Out or
out-of-sample test. The training data
consists of all the earlier data from 1959 Q2 up to the onset of the Hold Out
period. Thus, for the
Dot.com period,
the training data runs from 1959 Q2 to 2000 Q1.
The
quarters highlighted in orange denote recessions. We call the three periods, Dot.com, Great
Recession, and COVID periods as each respective period covers the mentioned
events.
To visualize the models' respective prediction performance, we will use "skylines." The column graph
below looks like a set of skylines with vertical buildings for positive values and reflection in water for
negative values. Within the complete linked study, we show several other ways to convey the forecasting
performance that you may prefer.
As shown above, all the models predictions are really pretty dismal. None of the models predicted the
protracted 3-year Bear market associated with the Dot.com bubble. At the margin, the OLS model
actually performed a bit better than the DNN models.
Now, let's look at the Great Recession period. In this situation, the models did better. However, their
overall predicting performance was nothing to write home about. All models completely missed the
severe market correction in the third year of the Great Recession period. And, again the DNN models did
not perform any better than the OLS Regression.
When focusing on the COVID period, the ongoing mediocrity (at best) of the models' prediction
performance is readily apparent. All models completely missed the robust Bull market in the third year of
the COVID period (as defined). Again, the DNN models did not fare any better than the simpler OLS
Regression.
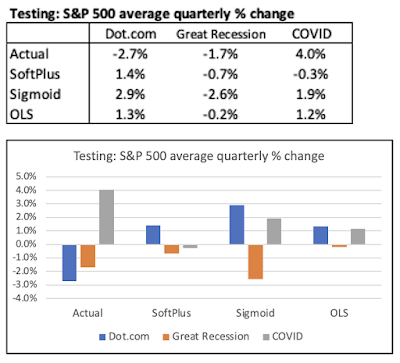
If we look at average predictions for all three models for all three testing periods, we can get a quick
snapshot of the competitiveness of the models.
Without getting bogged down into attempting to fine tune model rankings between these three models, we can still derive two takeaways.
The first one is that the Sigmoid issue with the "vanishing gradient descent" did not materialize. As shown, the Sigmoid DNN model actually was associated with greater volatility in average S&P 500 quarterly % change than for the SoftPlus DNN model.
The second one is that the DNN models did not provide any prediction incremental benefits over the simpler OLS Regression.
So, why did all the models, regardless of their sophistication, pretty much fail in their respective predictions?
It is for a very simple reason. All the relationships between the Xs and Y variables are very unstable. The table below shows the correlations between such variables during the Training and Testing periods. As shown, many of the correlations are very different between the two (Training and Testing). At times, those correlations even flip signs (check out the correlations with the Yield Curve (t5_ff)).
The models' predictions failing is especially humbling when you consider that the mentioned 3-year Hold Out tests still presumed you had perfect information over the next 3 years regarding the four X variables. As we know, this is not a realistic assumption.