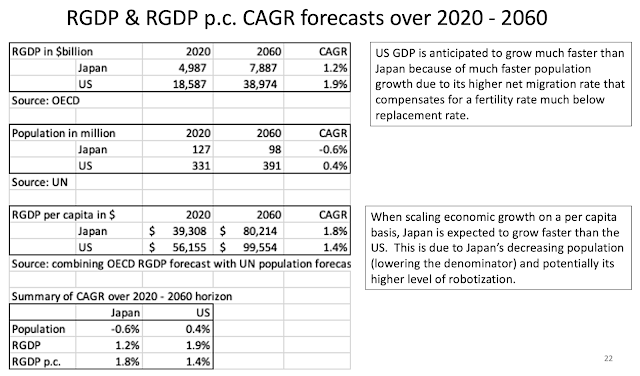
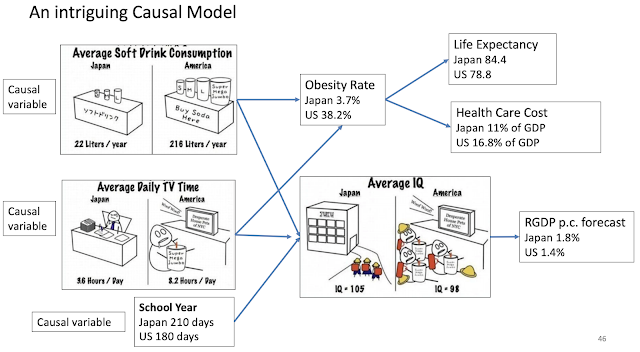
The short answer is not yet. The graph below shows that 2-points still make over 50% of overall points. Granted, 3-points have steadily risen since the 1979-1980 NBA season when 3-points were first introduced in the NBA. It took a while for the players to adapt their skills and coaches to evolve their strategies to leverage the benefits of 3-points shots.
The big difference over time is how much more aggressive players have become in attempting 3-points shots. Until the 2011 - 2012 season, teams were attempting less than twenty 3-points shots per game. The number has exploded to over 35 during the most recent two seasons.
Something to keep in mind is that the 3-points shooting skill of a team has only a rather moderate to weak relationship with a team's overall performance or ranking. And, that is another way to consider that 3-points shooting is not dominant in the NBA or even determinant in NBA team's success.
The graph above (using the NBA 2020-2021 season data) indicates that 3-points ranking of a team explains only 15% of the variance in the overall ranking of a team (R Square = 0.1485) and vice versa. If 3-points ranking explained 100% of the overall ranking, the red regression trend line would be perfectly diagonal across the squares on the grid. And, the regression equation would be: y = 1(x) + 0. Or in plain English: 3-points ranking = Overall ranking. As shown, this is far from this situation.
Here are the top 5 leaders in 3-points baskets.
Notice that two of them are still active: Stephen Curry (33 years old), and James Harden (32). One would expect Curry to soon become the top leader; and, James Harden to move into the third spot. By the end of their respective career, Curry and Harden may very well occupy the top 2 spots.
A closer look at the top 5 record on a per game basis.
What tables A and B indicate is that the contemporary players (Curry and Harden) have been far more productive in scoring 3-pts shots. And, the main reason behind their success is that they have been far more aggressive in attempting 3-pts shots (see table B).
In terms of accuracy (table C for 3-pts success rate), Kyle Korver, a player from another generation pretty much towers over the field. But, his higher success rate did not matter much given that he made so fewer 3-points attempts per game than Curry and Harden (see table B).
Curry's 3-points talent is in good part not reflected in any of the above statistics. Curry differentiates himself from the field with his unique ability to score 3-points baskets from "way downtown", often at or even past mid-court. Unfortunately, this superlative achievement is not rewarded with any scoring points benefits.
Harden is a very different player. While nearly as aggressive as Curry in attempting 3-points shots (table B). He is not nearly as accurate (lower success rate as shown in table C). In recent seasons, Harden has also somewhat lessened his focus on 3-points shots attempts (table B). On the other hand, Harden is a very dynamic and diversified player. And, his claim to fame may not be just his 3-points shooting skills, but his mesmerizing dribbling across his legs in a crouching tiger type position that has rendered him the most "unguardable" player in the NBA.
Next question worth considering is how long can we expect Curry to perform at top level in 3-points shooting?
Well, the short answer is for a pretty long time. The graph below shows the record of Ray Allen, Reggie Miller, and Kyle Korver who rounded the top 5 in 3-points shooting. We looked at their 3-points success per game (number of baskets) and their related success rate. The graph shows their respective performance as they aged. We used the average of their respective performance over 6 seasons when they were from 28 to 33 years old. We used this average as a baseline index = 100. And, next we divided each year specific performance by the 28 -33 average and multiplied it by a 100. This allowed us to measure precisely how their respective performance declined as they aged beyond 33 years old.
The left hand graph shows that Miller and Korver maintained their 3-points success per game very well as they aged. At 38 years old, they were still performing at 80% of their average level at 28 to 33 years old.
The right hand graph shows that all three players maintained their respective 3-points success rate remarkably well as they aged. Shooting accuracy just does not seem to deteriorate with age.
Curry is now 33. In view of the above, it is rather likely that he would be very close to or at top form over the next three years (34, 35, 36). Beyond 36, he may experience a mild decline in 3-points success per game. But, he may still be relatively formidable in that category compared to other players.
We could say the same thing for Harden (32). However, Harden has apparently been much less focused on 3-points shooting during the most recent two seasons.
I actually do not follow basketball. Seeing everyday pictures of Curry on the cover of the sport page of my daily newspaper, I eventually caught Curry fever. In view of that, I welcome comments, corrections. And, I would gladly edit and improve this blog entry over time.
If you want to read my complete study on the subject, check the two links below.