2022 Q1 GDP growth was already negative. And, 2022 Q2 may very well be [negative] when the released data comes out.
The majority of the financial media believes we are already in a recession because of the stubbornly high inflation (due to supply chain bottlenecks) and the Federal Reserve aggressive monetary policy to fight inflation. The policy includes a rapid rise in short-term rates, and a reversing of the Quantitative Easing bond purchase program (reducing the Fed’s balance sheet and taking liquidity & credit out of the financial system). The Bearish stock market also suggests we are currently in a recession.
On the other hand, Government authorities including the President, the Secretary of the Treasury (Janet Yellen), and the Federal Reserve all believe that the US economy can achieve a “soft landing” with a declining inflation rate, while maintaining positive economic growth.
The linked presentations include two explanatory models to attempt to predict recessions.
The first one is a logistic regression. The second one is a deep neural network (DNN). Both use the same set of independent variables: the velocity of money, inflation, the yield curve, and the stock market.
A copy of one of the slides describes the Logistic Regression model below.
A foundational equality: Price x Quantity = Money x Velocity of money
The logistic regression to predict
regression includes Price (cpi) and Velocity (velo). As the CPI goes up, the probability of a recession increases and vice versa. As the velocity of money goes up the probability of a recession decreases and vice versa.
This model also includes the yield curve,
a well established variable to predict recession. Notice that this variable is not quite
statistically significant (p-value 0.14).
But, the sign of the coefficient is correct. It does inform and improve the model. And, is well supported by economic theory. When the yield curve widens the probability of a recession goes down and vice versa.
The model includes the stock market (S&P 500) that is by nature forward looking in terms of economic outlook. This makes it a most relevant variable to include in a regression model to predict recessions. When the stock market goes up, the probability of a recession goes down and vice versa.
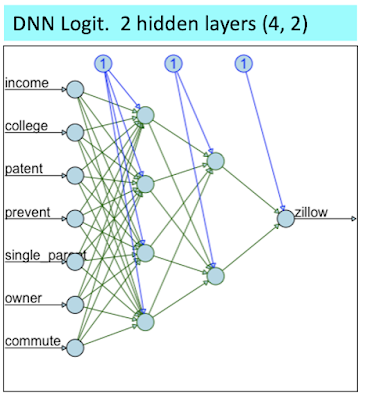
The deep neural network (DNN) model is described below.
The DNN model uses the same explanatory variable inputs.
The DNN model has two hidden layers with 3 neurons in the first one, and 2 neurons in the second one.
Number of neurons is nearly predetermined as hidden layers must have fewer neurons than the input layer and more neurons than the output layer.
The activation function is Sigmoid, which is the same as a Logistic Regression. And, the output function is also Sigmoid. This makes this DNN consistent with the Logistic Regression model.
I noticed that when using the entire data (from 1960 to the present using quarterly data), ROC curves and Kolmogorov - Smirnov plots did not differentiate between the two models. I am just showing the KS plots below. The two plots are very similar, not allowing you to clearly rank the models.
The next set of plots more clearly differentiate between the two models.
On the plots above, the recessionary quarters are shown in green, and the others are shown in red. You can see that the DNN generates nearly ideal probabilities that are very close to 1 during a recession, and very close to Zero otherwise. The Logistic Regression model generates a much more continuous set of probabilities within the 0 to 1 boundaries. Notice that both models do make a few mistakes with green dots (indicating recessions), when they should be red.
The graph above displays how much more certain the DNN model is.
All of the above visual data was generated using the entire data set. Next, we will briefly explore how the models fared when predicting several recessionary periods treated as Hold Out or out-of-sample if you will.
Let's start with the Great Recession.
As shown above, during the Great Recession period, the Logistic Regression was a lot better at capturing the actual recessionary quarters. It captured 4 out of 5 of them vs. only 2 out of 5 for the DNN.
Next, let's look at the COVID Recession period.
The above shows a rather rare occurrence in econometrics modeling, a perfect prediction. Indeed, both models with much certainty predicted all 6 quarters of this COVID Recession period correctly. And, as a reminder, these 6 quarters were indeed treated out-of-sample.
Next, we will use a frequentist Bayesian representation of both models when combining all the recession periods we tested (on an out-of-sample basis).
We can consider that recession is like a disease. And, given a disease prevalence, a given test sensitivity and specificity, we can map out the actual accuracy of a positive test or a negative test. Below we are doing the exact same thing treating recession as a disease.
Here is the mentioned representation for the Logistic Regression.
As shown above, during the cumulative combined periods there were 13 recessionary quarters out of a total of 30 quarters. And, the Logistic Regression model correctly predicted 10 out of the 13 recessionary quarters.
And, now the same representation for the DNN.
A table of these accuracy measures is shown below.
When you use the entire data set, the DNN is marginally more accurate. When you focus on the recessionary periods on an out-of-sample basis, the two models are very much tied.
So, can these models predict the current prospective recession?
No, they can’t. That is for a couple of reasons:
First, both models have already missed out 2022 Q1 as a recessionary quarter. Even using the historical data (not true testing), the Logistic Regression model assigned a probability of a recession of only 6% for 2022 Q1; and the DNN assigned a probability of 0%. Remember, the DNN is always far more deterministic in its probability assessments. So, when it is wrong, it is far more off than the Logistic Regression model.
Second, for the models to be able to forecast accurately going forward, you would need to have a crystal ball to accurately forecast the 4 independent variables. And, that is a general shortcoming of all econometrics models.